Where does Einstein need Quantum Mechanics?

|
his gravity law to extended objects. |
|
|
|
in the hydrogen atom. |
When Einstein invented his special relativity 1905, he must have thought about Lorentz-boosting extended objects. However, there were no physical processes where this effect could be observed. Even for point particles, the time dilation and space contraction were not experimentally established until mesons were discovered from cosmic rays.
Of course, like Newton, people have investigated the possibility of rigid spherical balls, and there are some published papers on this subject. I once checked those papers, but I am not able to present a comprehensive review at this time.
- The question is how the localized hydrogen wave function looks to your
friend on his bicycle. One technical difficulty is that the Lorentz
boost along a given direction, and is one dimensional problem, while the
hydrogen wave function is constructed in the spherical coordinate system.
While struggling with this difficulty, I read in 1970 one of the papers by Leopold Infeld (1898-1968) worrying about standing waves in a cubical box. Infeld is of course an important person in relativity who once collaborated with Einstein at Princeton (1936-38), but I am not able to give the exact reference to the paper I read. Please tell me know if you know what paper I am talking about.
-
Leopold Infeld (1898-1968),image from Wikimedia.
From his paper, I got the idea that
- a rigid body should be replaced by a localized standing wave, and that
- the coordinates should be separable in the Cartesian system.
-
Thanks to Wigner's influence on me,
I was able to see at least the
following point.
In his 1939 paper,
Wigner worked out internal
space-time symmetries of relativistic particles. According to him,
the symmetry of a given massive particle is like the three-dimensional
rotation group, which can best be represented by spherical harmonics.
Do you know how to Lorentz-boost those harmonics?

I was then able to realize that the three-dimensional harmonic oscillator is also separable in the Cartesian system, and I then found out I was not the first one to see this point.

-
Robert Hofstadter, image from
Douglas Hofstadter (his son). - In 1953, Hedeki Yukawa published a
short note in the Physical Review
containing a Lorentz-invariant harmonic oscillator equation for
relativistic extended particles. It is not cleatr whether he reported
his result to Einstein at their meeting in Princeton. Perhaps not.
Einstein's health was deteriorating at that time.
So far, we have been talking about mathematical ideology. The question is whether there are extended objects moving fast enough to be relativistic. Even for point particles, effects of special relativity were not obseved until mesons were observed during the 1940s.
- For extended objects, Hofstadter's experiemt
(published in 1956) demonstrated that the proton is not a
point particle, and it has a non-zero charge radius. This means that
the proton has a space-time extension. Since the proton can be acceleated
to relativistic speed, it can serve as the example for extended objects
in Einstein's Lorentz-covariant world.
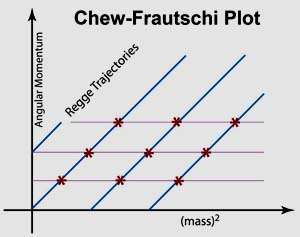
Among non-field theoretic models, we can mention Goldberger's dispersion relations, Chew's Regge poles, Chew-Frautschi plot, Chew's bootstraps. Chew's models are not derivable from quantum field theory, but his models were designed to follow the experimental developments.
- Thanks to those observations, Murray Gell-Mann in 1964 came up with the
idea of quarks. According to his quark model, the proton is a bound states
of three qaurks. Likewise all other hadrons are bound states of quarks and
antiquarks. Gell-Mann was able to explain all those hadrons in terms
of quantum numbers of the quarks.
How about the dynamics of bound states? Many people used non-relativistic quantum mechanics to hadrons as bound states of the quarks as they did to understand nuclei as bound states of nucleons. They produced numbers and published many papers.
- In 1970, Feynman gave a talk at the spring meeting of the American
Physical Society in Washington, DC, and I listened to his talk carefully.
He then
published his talk with his student in 1971..
- This paper contains one equation which accommodates both the
Klein-Gordon equation for the hadron and the oscillator
equation for the quarks inside the hadron.
- The oscillator excitations determines the mass spectrum,
and the rotational degeneracy reproduces Regge trajectories in the
Chew-Frautschi plot.
- While their differential equation is Lorentz invariant, their solutions are wrong. They do not produce localized bound-state wave functions.
- This paper contains one equation which accommodates both the
Klein-Gordon equation for the hadron and the oscillator
equation for the quarks inside the hadron.
- This lack of mathematical perfection does not prevent us from looking
further into their equation. Their partial differential equation can be
separated into more than 200 coordinate systems. Simply find a correct
coordinate system and continue the work. Thomas Edison's phonograph was
a crude device. This is the reason why people are still trying to
improve the quality of sound reproduction.
With one of the solutions of their 1971 equation, we can draw the following figure, and do more physics. Click on this figure for details.

Indeed, this leads to a Lorentz-covariant picture of extended objects as Einstein's one formula for the energy-momentum relation for massive and massless particles.
It is a pleasure to place the photos of Infeld and Hofstadter on this webpage. I met Robert Hofstadter several times, and he was very kind to me. I was too young to meet Infeld, but
I like his country.
- If you think I should post your photos on my future webpages, please do not
hesitate to contact me at yskim@umd.edu. If you have a better photo of
Infeld, I would like to have it.
Speaking of photographs, Orren Jack Turner (1920-2008) was an American soldier during World War II. After the war, he inherited his father's photo studio in Princeton, and took this photo of Einstein in 1947 (Einstein was 68 years old). He later donated his copyright of this photo to the U. S. Library of Congress, and the photo is in the public domain.
- I am very happy to tell you that the same photographer took a photo of
myself with my father the day before my commencement in 1961.
Like to see the photo?
Y.S.Kim (January 2010)
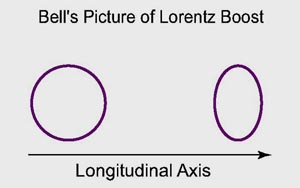
In his book entitled "Speakable and unspeakable in quantum mechanics," J. S. Bell attempted to explain the Lorentz boost of the electron orbit in the hydrogen atom in terms of a circle and ellipse, but I do not know how to write the orbit formula in a Lorentz-covariant form.
You would recall that this hydrogen orbit could be replaced by a standing wave in accordance with the wave-particle duality. The question then is whether this makes the problem any easier. Indeed, we do not yet have a statistically description of Lorentz-covariant wave functions of the hydrogen atom.
- copyright@2010 by Y. S. Kim, unless otherwise specified.

| |
|