Conic Sections

Click here for the source of this drawing.

Here is a photo of two Russian ladies at the Lake Sevan, Armenia taken in 1998. One of them is Valentina Novikova who was responsible for taking care of foreign visitors to the JINR in Dubna (north of Moscow). She is well known among those who have visited Dubna. You can recognize her in this photo. This photo was taken in 2000 while I was attending a conference held in Dubna.

• The other lady was wearing a cone-shaped Vietnamese hat. What physics can you extract from her hat? I am not the first person to ask this question.

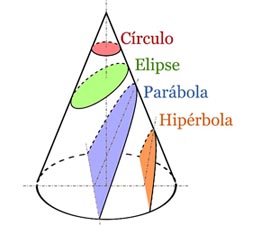
• Greek observed there are three different curves, namely circle (ellipse), hyperbola, and parabola. They then believed that they should come from one source. Indeed, a circular cone provides all of these curves.

  Greeks believed that there are three fundamental elements in one thing. For instance, they thought one ideal woman consists of three different women carrying their respective virtues. Click here for a detailed story.

• Some years later, Isaac Newton formulated the law of gravity and his second order differential equation. In so doing, Newton was able to unify elliptic, hyperbolic, and parabolic orbits. This aspect of physics is well known.

  Step 1, Step 2.

• Click here for a more detailed story about how Newton defined the history of physics. Quantum mechanics was formulated to answer the question of why energy levels are discrete for the hydrogen atom while the Rutherford scattering formula is applicable to the electron-scattering. Here again, quantum mechanics was formulated to unify the elliptic orbits of the electron and the hyperbolic trajectory in Rutherford scattering. This aspect of modern physics is also well known.

• Don't forget Einstein. Thanks to Feynman diagrams, we have a good idea of the hyperbolic trajectories (scattering problems) in the Lorentz-covariant world. How about the hydrogen atom with discrete energy levels? How would this atom look to an observer on a bicycle?
  1. This is John Bell's has this picture of the Lorentz-boosted hydrogen orbit in his book. This picture however does not explain why the its energy levels are discrete.
  2. Standing waves. How to Lorentz-boost?
  3. Evolution of the hydrogen atom the proton in the quark model.
  4. Quarks and Partons as two limiting cases of one Lorentz-covariant entity.

• Internal Space-time Symmetries. The first step toward what is going on inside the proton is to understand the internal space-time symmetries of particles in the Lorentz-covariant world. If the particle is at rest, then it has the symmetry of the three-dimensional rotation group. If the particle gains its speed, we have to worry about additional degrees of freedom.
  1. In his 1939 paper, Wigner formulated this problem in terms of his little groups. The Lorentz group has six degrees of freedom. If the four-momentum of a particle is fixed, it has only three degrees of freedom, defining internal space-time symmetries. For a massive particle at rest, it has three rotational degrees of freedom. corresponding to the spin degrees of freedom.

     If you like to have a reprint of Wigner's 1939 article, send your reuest to yskim@umd.edu.

  2. For massless particles, the problem was not completely solved until 1990. In his original 1939 paper, the internal space-time symmetry is isomorphic to the two-decisional Euclidean group. The rotation corresponds to the helicity of the particle. There are two translation-like degrees of freedom. It was later suggested by various authors that they correspond to a gauge degree of freedom. However, why the one-parameter gauge degree of freedom corresponds to two translational degree of freedom. This question is addressed in the 1990 paper of Kim and Wigner.

  3. If the particle mass is imaginary, it moves faster than light, and is thus not observable. Yet, recent trends in physics allow us to talk about this possibility.

  4. Indeed, the transformation groups leaving those momenta invariant are like O(3) (circle), like E(3) (linear or quadratic), and O(2,1) (hyperbolic) respectively. Again the conic sections dominate even inside the particle.

  5. In spite of this simple picture of Wigner's view toward the internal space-time symmetries, his 1939 paper is regarded as one of the most difficult papers to understand. Yes, there have been and there still are many rising stars in physics who claimed to have solved the poblem of internal space-time symmetries. However, they carefully avoid Wigner's classic paper on this problem. In so doing they are missing the main point, and those stars fall down. Wigner's 1939 paper appears to be the prescrition for their longevity.

  6. Sakura is the Japanese word for cherry blossom. During a one-week period of spring every year, the city of Washington (capital city of USA) becomes brightened by full-blown Sakura flowers. I am indeed fortunate to live near this city to enjoy this Sakura phenomenon every year.

     However, the problem is they do not last too long, they disappear one week after their peak showing. It would be nice if someone could invent a botanic process to make them last longer. Likewise, the physics community is blessed with those Sakura-type physicists. We only wish they could stay longer to give us prolonged excitements.

• Post-Wignerian Approach. Wigner's original paper divides the particle symmetry into three distinct classes. However, we can approach the problem as one symmetry with three branches. This viewpoint can be derived from our experience in ray and polarization optics. Modern optics is largely a physics of two-by-two matrices from the group SL(2,c). The generators of this group share the same set of commutation relations with those for the group of four-by-four matrices performing Lorentz transformations. For this reason, we can study Wigner's little groups, or internal space-time symmetries, using optical instruments and two-by-two matrices.

  1. Here is a review article on this subject. It is easy to read this paper because it contains only two-by-two matrices. The only non-trivial aspect of this paper is that not all those two-by-two matrices can be diagonalized. The question is how to deal with it.

  2. I spent some years on this subject, and learned many lessons while writing papers with my younger colleagues. We learned the most important lessons from those referees who attempted to turn down our papers. For instance, we learned how to use the traces of two-by-two matrices in our logic from one of the hostile referees. It is my pleasure to thank them for writing those valuable reports for us.

• Let us choose a real positive number. It can be smaller than two, equal to two, or greater than two. It is so simple that even God can say this. Then God created elementary particles using two-by-two matrices.

Click here for his home page.