Why am I regarded as Wigner's student?
Before Newton, physicists tried to find physical laws by looking at the sky. People still do. Do you know how many stars there are in the sky? These days, there are the same number number of physics papers to read. Thus, some physicists try to find something new from those papers.
- For massless particles, Wigner observed the symmetry group is isomorphic
to the two-dimensional Euclidean group or E(2), consisting of one rotational
and two translational degrees of freedom. It is easy to associate the
rotational degree to the helicity. What about the translational degree of
freedom? This question was not completely addressed until 1990, 51 years
after 1939.
Thus, this is an interesting topic in history of physics. In 1939, Wigner stated that the symmetry is isomorphic to E(2) and wrote down the matrix of this form.
-
This ugliest matrix in physics is contained in Wigner's 1939 paper.
This matrix used to scare away young physicists who wanted to understand
this paper.
- This is the "ugliest" matrix in physics. Even these days, physicists
give up if the matrix is not unitary. I know this from my
own experience. Since 1973, my papers were based on non-unitary squeeze
matrices. Did you know that Lorentz boosts are squeeze transformations?
As soon as I start telling this, my colleagues run away from me.

-
Weinberg talking to Wigner (1957). Photo by Dieter Brill.
- Steven Weinberg had a great respect for Wigner, and he published the
following papers on Wigner's 1939 paper.
- S. Weinberg,
Phys. Rev. 133, B1318 (1964).
- S. Weinberg,
Phys. Rev. 134, B882 (1964).
- S. Weinberg, Phys. Rev. 135, B1049 (1964).
While studying these paper written by Weinberg, with my younger colleagues named D. Han and D. Son, came up with the idea of two-dimensional Eucliedean plane with one rotational and two translational degrees of freedom as shown in this figure. We published this result in the followingg papers.
- D. Han, Y. S. Kim, and D. Son, Phys. Rev. D 25, 461 (1982).
- D. Han, Y. S. Kim, and D. Son,
Phys. Rev. D 31, 328 (1985).
This two-dimensional figure tells about rotations and translations in the E(2) plane, and the translations as gauge transformations. As for the issue of gauge transformations, there are several other authors who said the translations correspond to gauge transformations, and they were quoted in my papers. Most certainly, I am not the first one to observe this aspect of Wigner's E(2)-like symmetry.
-
Photon spian and gauge degrees of freedom in the two-dimensional plane.
- A. Janner and T. Jenssen, Physica 53, 1 (1971); ibid. 60, 292 (1972).
- K. Kuperzstych, Nuovo Cimento B 31, 1 (1976).
- S. Weinberg,
Phys. Rev. 133, B1318 (1964).
- This is not enough. If the massless particle has the symmetry of two-dimensional
plane, while the massive paricle has the three-dimensional shperical symmetry,
the two-dimensional plane could be a portion of the spherical surface in the
large-radius limit, like the map of a city. The radius could be associated
with the speed of the particle. This means that the the E(2)-like little
group could be a limiting case of the O(3)-like little group of the massive
particle.
- D. Han, Y. S. Kim, and D. Son, Phys. Lett. B, 131B, 327 (1983).
- D. Han, Y. S. Kim, and D. Son, J. Math. Phys. 27, 2228 (1986).
In arriving at this conclusion, we used the technique of group contractions intoroduced first by Inonu and Wigner in 1953 [E. Inonu and E. P. Wigner, Proc. Natl. Acad. Sci. (U.S.) 39, 510 (1953)]. The idea is very simple. For a curved line, there is a tangent line. Likewise, there is a tangential pane for a curved surface such as a spherical surface. We experience this everyday on the surface of the earth.
This table was included in one of the papers listed above, namely this paper.Contents of Einstein's E = mc2 Particle Variables Massive/Slow between Massless/Fast Einstein
Energy
MomentumE=p2/2m Einstein's
E=(m2 + p2)1/2E= cp Wigner Helicity
Spin, GaugeS3
S1 S2Winner's
Little GroupHelicity Gauge Trans. - After seeing this, I thought the person who would appreciate this most
was Eugene Wigner who wrote the above "ugly" matrix in his 1939 paper.
In 1985, I went to Princeton to tell him about the translation-like
variables in his E(2)-like group. He became very happy, but asked why
there have to be two gauge components ( x and y coordinates).
I then had to work hard to make Wigner happy. I pulled out Wigner's 1953 paper with Inonu on group contractions, telling that a spherical surface can become flat if the radius becomes large. Thus, we can consider a tangential plane for the E(2) symmetry.
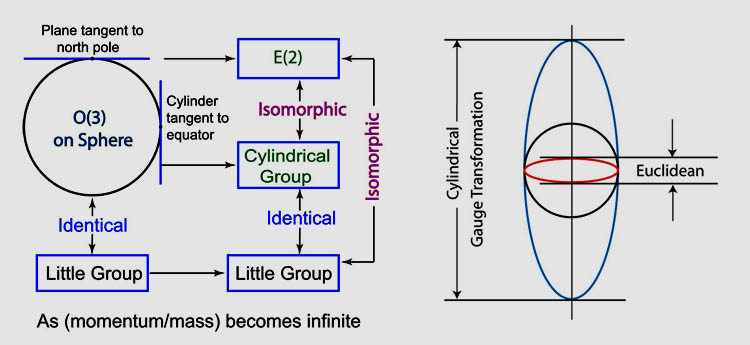
The E(2) symmetry comes from the plane tangential at the north pole, while the cylindrical symmetry comes from the cylinder tangential at the equatorial belt (left figure). Click here for the 1987 paper by Kim and Wigner.
The four-by-four Lorentz transformation matrix produces a geometry which deforms a sphere into an egg and a pancake, which eventually become a cylinder and a plane respectively. Click here for the 1990 paper by Kim and Wigner. - Indeed, both translation-like variables correspond to one up-down translation
on the cylindrical surface. Thus, Wigner's E(2)-like symmetry has one
rotational degree and one translational degree of freedom. This translational
degree of freedom corresponds to the gauge degree of freedom.
During the period of five years (1985-90), I went to Princeton frequently to seek guidance from Eugene Wigner. I was like a graduate student working on his thesis research under Wigner's guidance.
- These days, I am frequently introduced as Wigner's youngest student,
while my thesis advisor was Sam Treiman
when I got my PhD degree in 1961. I wrote my thesis on the subject
of "dispersion relations" which led to the fantasy that physics comes from
singularities in the complex plane.
In 1966, while I was an assistant professor at the University of Maryland, I showed how stupid this fantasy was. I then decided to continue studying Wigner's 1939 paper. I started reading this paper when I was a graduate student at Princeton, and I had the privilege of asking questions to Professor Wigner.

|
|
copyright@2014 and 2021 by Y. S. Kim, unless otherwise specified.
- Click here for his home page.
- His photo-biography.
- His Einstein page.
- His Princeton page.
- His Style page.
|

