Physics based on ellipse and Hyperbola
- Conic sections.
- Group contractions.
- Lorentz harmonics and squeeze harmonics.
- Two-by-two matrices.
- Physics of the Lorentz Group, my latest book with S. Baskal and M. E. Noz. The title page of this book contains the figure
Group Theoretical Approach to Physics
-
The most familiar group in physics is the rotation group governing
rotations in three-dimensional space. These rotations are norm-preserving
transformations. This concept is then extended to unitary groups governing
unitary transformations in quantum mechanics. These groups are also
well known.
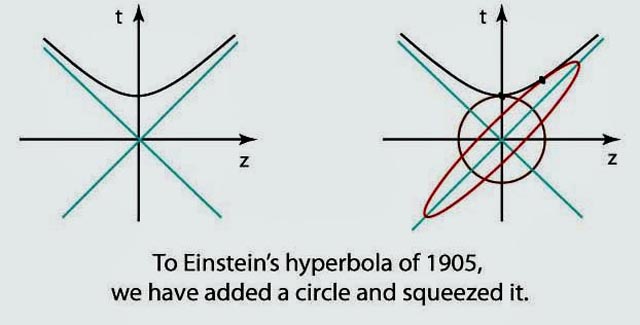
I have been and still am interested in transformations which will transform a circle into ellipse, a square into a rectangle, and a sphere into an ellipsoid. It is quite natural to call these squeeze transformations. You will be surprised to hear that Lorentz boosts are squeeze transformations, as illustrated in the following figure.
To many people, I am known as Wigner's youngest student. Yes, I got my PhD degree from Princeton University in 1961. My thesis advisor was Sam Treiman, but I later wrote many papers to make Eugene Wigner happy.

|
Have you seen this picture?
-
This picture came from a paper which I published with
M. E. Noz and S. H. Oh, in
J. of Math. Phys. in 1979 (Vol. 20, page 1341).
For an earlier version of this
figure telling the same physics, see Y. S. Kim and M. E. Noz,
Phys. Rev. D 8, 3521 (1973). The picture tells you
that Lorentz boosts are squeeze transformations.
Based on the papers I have published with my co-authors, I have written a book with Marilyn Noz on applications of the Poincaré group to particles physics. In this book, we deal with Lorentz boosts of extended objects. This picture of Lorentz boost allows us to construct a covariant theory where the quark model and the parton model are two different aspects of one covariant theory.
It is often more convincing to explain what I did in terms of what others say about what I did.
Mathematical Reviews
-
January 1988
88a:22037 22E70 81C40.
Kim, Y. S. (1-MD-R); Noz,Marilyn E. (1-NY)
Theory and applications of the Poincaré Group.
Fundamental Theories of Physics.
D.Reidel Publishing Co., Dordrecht - Boston, Mass, 1986.
xvi+331 pp. $73.00. ISBN 90-277-2141-6
This book deals mainly with the applications of the Poincaré group in high energy physics. But the authors also give an introduction to group theory, making use of the physical applications to illustrate and show how the theory works. The material contained in this book is divided into twelve chapters.
The first two introduce the basic elements of group theory. The second of them presents Lie groups and Lie algebras. The following chapter studies the group of Poincaré and its representations, paying special attention to the transformation of wave functions and fields. The theory of spinors is developed in Chapter IV; the group SL(2,C) is studied in detail.
So far all the material presented can be found in many other books. Nevertheless, from Chapter V on the approach of the book is more original. The authors deal with concrete physical applications of the Poincaré group, following in some cases ideas developed by them in papers mainly published in the American Journal of Physics of recent years.
Firstly the harmonic oscillator in a covariant formalism is studied. This is discussed in the following chapter where hadronic theory is presented dealing with Dirac's ideas of relativistic quantum mechanics. Later, in the last two chapters of the book, some applications of this oscillator formalism to hadronic phenomenology are given, for example, to give an explanation of the mass spectra of hadrons and the study the deformation properties of relativistic hadrons.
Chapter VIII deals with massless particles, making a detailed analysis of the little group of such particles (isomorphic to the two-dimensional Euclidean group E(2)). The next chapter is dedicated to contraction of groups. The idea is to show the relationship between the little groups of massive and massless particles (isomorphic to O(3) and E(2), respectively). Finally, the two remaining chapters deal with the representations of the groups SO(2,1) and SO(1,1) and SO(3,1).
Note that E. P. Wigner's noteworthy paper [Ann. Math. (2)40 (1939), 149-204; Zbl 20, 296] was the source of inspiration for the authors when writing this book. There is also a remarkable trace of some of Dirac's papers in this book.
The book presents a very good collection of problems places at the end of each chapter.
--- Mariano A. del Olmo (Valladolid).