Further Contents of E = mc2
Albert Einstein was born in Ulm (Germany) on March 14, 1879. However, his family moved to Munch when he was an infant. There, his family set up a profitable business of manufacturing electric appliances. However, due to the AC revolution, their business became bankrupt.- Einstein's family had to move to a small town near Milan (Italy).
In 1895, at the age of 16, Albert went to Switzerland. There, he finished
his high-school education. Two year later in 1897, Einstein entered Zürich
Federal Polytechnic for his 4-year college program. This school is known
today as ETH
(Eidgenössische Technische Hochschule).
Like all young physicists these days, Einstein had difficulties in finding a job, but he managed to get a position at the Swiss patent office in Bern, and moved to Bern in 1901. There he married his former female classmate named Mileva Maric in 1903.
Einstein in 1904 or 1905

Birth Place of E = mc2 
In this house, during the years
1903-1905, Albert Einstein created his fundamental treatise on relativity theory. - While working for the patent office, Einstein pursued his physics research
and completed his special theory of relativity. He did not pull out
this revolutionary theory from the blue sky.
- During his high-school years, he was immensely interested in the
philosophy of Kant who said things could look differently to different
observers depending on where they are or how they think.
Click here for his philosophical
background.
- He was quite interested in the mathematics of Lorentz transformations
developed earlier by Lorentz and Poincaré. He also learned from
Hermann Minkowski that Maxwell's equations are covariant under Lorentz
transformations.
- He noticed the velocity addition rule is cumbersome in the Lorentzian
regime. He thus tried transformation laws for the momentum, and
came to the conclusion that the momentum and energy form a four-vector,
just like the space-time four-vector.
While
t2 - x2 - y2 - z 2
is an invariant quantity in the Lorentzian world, Einstein came to the conclusion that
E2 - px 2 - py2 - pz 2 = mass2 .
This is what Einstein's E = mc2 is all about.
This completes the energy-momentum relation for particles in the Lorentz-covariant world.
- During his high-school years, he was immensely interested in the
philosophy of Kant who said things could look differently to different
observers depending on where they are or how they think.
Click here for his philosophical
background.
What happens when the particle has internal space-time structures ?
- Bohr and Einstein met occasionally to discuss physics. Einstein was interested
in how things appear to moving observers. Bohr was interested in the electron
orbit of the hydrogen atom. Did they ever talk about how the electron orbit
looks to moving observers? This is still the most outstanding problem in
physics.
Isaac Newton had a similar problem when he formulated his law of gravity. He wrote down the formula for the inverse square law between two point particles. It then took him 20 years to complete the law for extended objects. He had to invent a new mathematics known today as "Integral Calculus," as shown in the following figure.
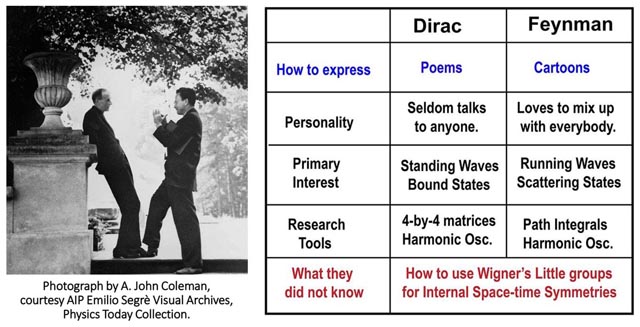
- Of course, many distinguished physicists worried about this problem. In the
following photo of Dirac and Feynman (Poland 1962), they are not communicating well.
I was fortunate to have an
audience with Dirac three months
after their meeting. Based
on what I heard from Dirac and
many years of research on their papers,
I am able to construct the following table.
It is a great challenge to interpret what Feynman is saying to Dirac, and what Dirac wants to say to Feynman. There are two possible ways.
- Translate Dirac's poems to cartoons Feynman can understand.
Click here for the cartoon.
- Translate both Dirac and Feynman into a common language. It is not clear whether Feynman was aware of Wigner's 1939 paper on his little groups. Dirac occasionally mentioned Wigner's paper, but made no attempts to interpret this work in terms of the little groups.
- Translate Dirac's poems to cartoons Feynman can understand.
Click here for the cartoon.
- Then what is Wigner's paper about?

This aspect of Wigner's work is yet to be recognized. - In 1939, Wigner constructed subgroups of the Lorentz group whose
transformations leave the momentum of a given particle invariant.

This book is available from - If the particle is massive, there is a Lorentz frame in which
the particle is at rest. In this frame, the momentum is invariant
under three-dimensional rotations. Thus, the little group is O(3) or
the three-dimensional rotation group. This indeed tells the spin
degree of freedom.
- In 1939, Wigner observed that the little group for massless
particles is isomorphic to E(2) or two-dimensional Euclidean group
with one rotational and two translational degrees of freedom. It
is easy to associate the rotational degree with the helicity of
the massless particle. What physics is associated with the
translations. This question was not completely settled until
1987. These two translational degrees of freedom collapse into
one gauge degree of freedom.
Click here for details.
- Einstein's the energy-momentum relation for the massive particle becomes the same as that for massless particle when its momentum is much larger than the mass. Likewise the O(3)-like little group for massive particle becomes the E(2)-like little group when the momentum of the particle is much larger than the particle mass. Click here for a published article.
- In 1939, Wigner constructed subgroups of the Lorentz group whose
transformations leave the momentum of a given particle invariant.

|
|
Did they ever talk about moving hydrogen atoms? |
Did you know that the Dirac equation is a representation of Wigner's
little group? Did you know the Maxwell tensor and four vector are
also representations of the little group?
Click here.
- We can organize these results in the following Einstein/Wigner table.

Einstein's Genealogy Massive/Slow between Massless/Fast Energy
MomentumE=p2/2m Einstein's
E=(m2 + p2)1/2E=p Helicity
Spin, GaugeS3
S1 S2Winner's
Little GroupHelicity Gauge Trans. Click here for a photo. Build
YOUR OWN HOUSE!You are then invited to build your own house. How are you going to build your own house? With what? In order to build a house consistent with it neighborhood is to find a Lorentz-covariant entity which takes different forms for slow and fast particles.
See next page.
portrait by Bulent Atalay (1978). photos of Bohr and Einstein from the AIP Segre Visual Archives.