Two different routes to Princeton

Wigner's Student at Princeton?, No but Yes.

• I brag about PhD from Princeton University. I was a graduate student there from 1958 to 1961. I stayed there for one additional year until 1962 as a postdoctoral fellow. My thesis advisor was Sam Treiman.

  Weinberg and Treiman (1985). Sam and Joan Treiman with my family (1987). My son went to Princeton (undergraduate), Treiman was also his teacher.

  He was a good teacher and taught me how to write stylish articles. He was the thesis advisor to Steven Weinberg, who remains as one of the most respected physicists of our time.

  People do not trust me when I say I shared the same adviser at Princeton, because Weinberg is so high and I am so low.

  Treiman also wrote good recommendation letters for me throughout my professional career. Needless to say, I am grateful to him.

  My son was in his quantum mechanics classes in 1986-87 when he was an undergraduate student at Princeton.

  There is thus every reason for me to brag about being Treiman's student while at Princeton.

  Yet, I am known widely as Wigner's student at Princeton.

• The story is somewhat complicated, but the simple explanation is that I published a number of papers with Wigner from 1987 to 1990, many years I left Princeton in 1962.

  While I was at Princeton (1958-62), the physics world was dominated by a belief that the origin of physics is the scattering matrix and its analytic properties in the complex energy and angular momentum planes. This belief created exciting words such as dispersion relations, N/D methods, Regge poles, and then bootstrap dynamics. I wrote my thesis on dispersion relations and published four papers on this subject before becoming an assistant professor at the University of Maryland in 1962.

• However, I sensed something wrong with this misguided belief. While still at Princeton, I started studying Wigner's 1939 paper published in the Annals of Mathematics.

  Like Einstein, Eugene Paul Wigner (Nobel 1963) was a historical figure in physics, but he was totally isolated from the rest of the physics department there. Younger professors told me not to waste my time on that useless paper. They told me Wigner is gone. At that time, I sensed there was something wrong with this environment.

• In 1965, while I was struggling as an assistant professor at the University of Maryland, Princeton found a genius of the century. His name was Roger Dashen. He was three years younger than I was, but was appointed as a full professor at Princeton's Institute for Advanced Study (institute created for Einstein).

  With my Herod complex, I could not afford anyone smarter than I was. I published my papers telling

  Dashen made a mistake in his calculation of the neutron-proton mass difference,

  but the reaction from the American physics community was thoroughly hostile toward me. The prevailing reasonings were

  1. Dashen is a genius, but you are only a Korean. Go back to Korea.

  2. Princeton is Einstein's place. How can anyone from Maryland challenge a genius at Princeton?

  Thus, my position in the United States was in danger. The only person who could save me was Sam Treiman who was my thesis advisor at Princeton, and I went to Princeton to explain the situation to him.

  However, Treiman's brain did not have enough resolving power to see the details of the mistakes Dashen made in his paper. He became very angry, and told me never come to Princeton again.

• There is another factor, perhaps the crucial factor. While I was a student there, Treiman routinely called me "oriental boy." This kind of presjudice still exists in the academic world even these days.
  How can an oriental boy challenge the American genius?

  This was the attitude I could see from his face.

• I heard that Treiman later changed his mind by realizing I was right from the public opinion. If he found about me from the public opinion (not directly from me), he was not a good advisor to me. He was a useless person to me. Thus,

  I had to find a different route to Princeton.

• In the meantime, my senior colleagues at Maryland realized the seriousness of my case and went through a through investigation of the case. They then decided I was right. This delayed my promotion to my tenured position by one year.

  The United States has been and very nice to me.

• This Dashen case led me to see why Eugene Paul Wigner (Nobel 63) was so isolated from the rest of Princeton.

  They did not have enough brain power to digest Wigner's 1939 paper on the Lorentz group, becase they could not reslove Dashen's case.

  Thus, I had to conclude that I am smarter than they are, and I should be able to do what they could not do.

• I then decided to understand the full implications of Wigner's 1939 paper, and tell Wigner what he wanted to hear. Here, I was guided by a
  piece of Korean wisdom.

  While I was publishing my papers on high-energy physics based on Gell-Mann's quark model and Feynman's parton picture, I was interested in how Wigner's 1939 paper was applicable to the quantum bound state moving with relativistic speed.

• By 1986, I felt that I published enough papers to tell the stories Wigner wanted to hear. I contacted him and started telling the stories he wanted to hear. He became very happy, happy enough to publish papers with me. This was how I started my collaboration with me and publish joint Kim-Wigner papers.

• Let us see the details of this Kim-Wigner collaboration.
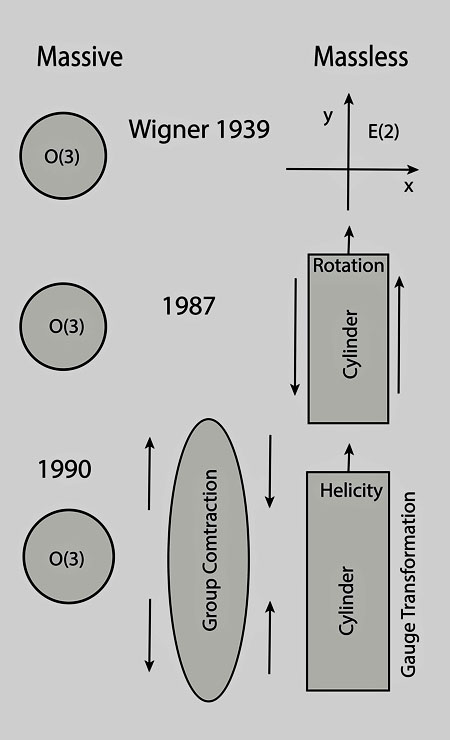
  1. In 1939, Winger published a paper on the little groups of Lorentz group. He noted there that the Lorentz group has six degree of freedom. For a particle, if its momentum is fixed, there are three remaining degrees of freedom. For a free particle with zero momentum, those three rotational degrees are for the spin of the particle.

     For the massless particle, the internal symmetry is like the two-dimensional Euclidean group with one rotational and two translational degrees of freedom. It is trivial to associate the rotational degree with the helicity of the massless particle. However, what physics do those two translational degrees mean? It was found that they correspond to a gauge degrees of freedom.

     I was not the first one to worry about this problem. Steven Weinberg published a series of papers on this subject.

  2. In 1987, Kim and Wigner showed that the Euclidean symmetry for the massless particles can be generated from the geometry of a circular cylinder with one rotational degree freedom for its helicity, and one up-down translation for one gauge degree of freedom.

  3. In 1990, Kim and Wigner noted that the three-dimensional sphere can give the three-dimensional rotation group. They noted also that the Lorentz boost can elongate this sphere in the direction of the boost. Thus, if the particle moves with its speed close that of light, the sphere becomes a cylinder. In this way, we can produce the following table for the internal space-time symmetry of the particle in Einstein's Lorentz-covariant world:

     Contents of Einstein's E = mc2

     Particle Variables Massive/Slow between Massless/Fast

     Einstein Energy Momentum E=p2/2m Einstein's E=(m2 + p2)1/2 E= cp

     Wigner Helicity Spin, Gauge S3 S1 S2 Winner's Little Group Helicity Gauge Trans.

     This table allows us to place Wigner next to Einstein:

     

  4. Let us go back to the table given above. It is easy to note that the internal space-time symmetry for the massive particle at rest is its spin angular momentum. However, the two-dimensional Euclidean symmetry for the massless particle has a stormy history. We should note the efforts made by the following authors.
     1. S. Weinberg, Phys. Rev. 133, B1318 (1964).
        
     2. S. Weinberg, Phys. Rev. 134, B882 (1964).
        
     3. S. Weinberg, Phys. Rev. 135, B1049 (1964).

     4. A. Janner and T. Jenssen, Physica 53, page 1 (1971), and Physica 60, page 292 (1972).

     5. J. Kupersztych, Nuovo Cimento B 31, page 1 (1976).

     Indeed, these authors noted that the two translational degrees of freedom lead to the gauge degree of freedom.

     However, why does one gauge degree of freedom require two translational degreea of freedom? Kim and Wigner in 1987 provided the answer to this problem by introducing the cylindrical symmetry as described above.

• My collaboration with Wigner made some famous people jealous and unhappy. They hehaved like beasts. Click here for your entertainment.