100 year ago
 |
| These photos are from the public domain. |
There are no hydrogen atoms moving with relativistic speeds. Thus, this Bohr-Einstein issue is only a metaphysical problem.
After 1950, high-energy accelerators produced protons moving with speed close to that of light, but the proton is not a hydogen atom.
On the other hand, while the hydrogen atom is a quantum bound state, the proton became a bound state in world of Gell-Mann's quark model. Thus, the proton can also play the role of quantum bound state. Unlike the hydrogen atom, the proton can be accelerated and its speed can become very close to that of light, as illustrated in this figure:
Feynman's Parton Picture

|
Five years later, in 1969, Richard Feynman observed that a hadron, when it moves with a speed close to that of light, appears as a collection of infinite number of partons with a wide-spread momentum distribution. Partons interact incoherently with external signals.
It is only natural to regard the parton picture as a Lorentz-boosted quark model. However, since the partons are so different from the quarks, we have been wondering whether they are really Lorentz-boosted quarks.
Thus, the Bohr-Einstein issue on the hydrogen problem becomes this quark-parton puzzle.
-
This file is very long. You may be interested in jumping to one of the
following specific isssues.
- Further Contents of E = mc2
- Covariant Model
- Lorentz Boost
- Feynman's Decoherence
- Infinite Number of Partons
- Boiling Quarks and Phase Transition
- Quantum Mechanics of Moving Bound States published in J. Modern Physics [13] 138-165 (2022).
Further Contents of Einstein's Energy-momentum Relation
- Click here for further contents
of Einstein's E = mc2.
- According to Feynman,
the adventure of our science of physics is a perpetual attempt to
recognize that the different aspects of nature are really different
aspects of the same thing.
If this is the case, we are doing the same physics whether we do the quark model or do the parton model. Indeed, ever since Feynman presented his parton model in 1969, one of the most pressing problems in high-energy physics has been whether it is possible to formulate a covariant theory which will produce the quark model for slow hadrons and the parton model for fast hadrons, within the framework of the existing rules of quantum mechanics and special relativity.
In this photo, one Feynman admirer is standing in front of Feynman's preterit at the entrance of the Feynman Computing Center at Fermi National Accelerator Center, Batavia, Illinois (June 2003). He has been doing Feynman's physics since 1970.
- According to Ne'eman, Feynman diagrams and
the parton model are the two greatest contributions Feynman made. Feynman
diagrams are well known and well understood, but his parton model is yet
to be understood. Why is it so difficult to understand the parton model?
It contains too much physics, including some of the current issues such as
decoherence, as well as future issues.
| ||||
| ||||
| ||||
|
How can we construct a covariant model for quarks and partons?
Let us start with a hadron consisting of two quarks bound together by a harmonic oscillator potential. The simplest wave function for this two-particle system is is the harmonic oscillator wave function. Can this wave function be Lorentz-boosted?
- Its boundary condition can be stated in terms of the spatial
coordinates in a given Lorentz frame. Then how about other frames
where the spatial and time-like coordinates are mixed?
In order to deal with this problem, we need the time-separation variable.
Does this variable exist? We are quite familiar with the Bohr radius.
It measures the spatial separation between the constituent particles.
Then, is there a time-like separation? According to Einstein, the
answer is YES. This is the starting point of our plan to construct
a harmonic oscillator wave function which can be Lorentz transformed.
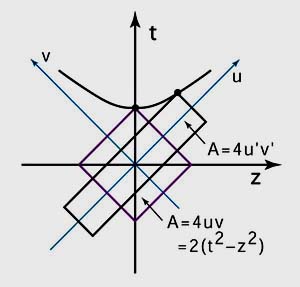
- Let us tackle this problem with the following three figures. The first
figure is a space-time diagram of the harmonic oscillator wave function.
The second figure describes Lorentz boosts in the light-cone coordinate
system. The third figure combines quantum mechanics with special
relativity by combining the first two figures.

-
Dirac 1927 (top) and Dirac (1949)
Synthesis of the above two figures.
- The present form of quantum mechanics.
Let us consider a hadron consisting of two quarks bound together
by a harmonic oscillator potential. Then, Heisenberg's uncertainty
principle applies to position-momentum coordinates,
and there are excited states along the space-like directions. As
for the time-like (time-separation between the quarks),
there are no excitations, but there still exist a time-energy uncertainty
without excitation. According to Dirac, it is a c-number time-energy
uncertainty relation.
- Special relativity. Lorentz boost in the light-cone coordinate system.
We are quite familiar with the condition
-
(z2 - t2) = constant
in special relativity. This equation gives the hyperbola in the graph. The above equation can also be written
-
(z + t)(z - t) = constant.
The Lorentz boost along the z direction expands (z + t) and contracts (z - t) while keeping the above product constant. This is called Dirac's light-cone coordinate system. The Lorentz boost is now a "squeeze" transformation.
- It is then easy to combine quantum mechanics and special relativity.
We can now Lorentz-boost quantum mechanics given in the first figure.
We can simply squeeze the circle given in the first figure according
to the transformation law of special relativity given in the
second figure.
- Einstein and Feynman. Dirac talks about them.
- The present form of quantum mechanics.
Let us consider a hadron consisting of two quarks bound together
by a harmonic oscillator potential. Then, Heisenberg's uncertainty
principle applies to position-momentum coordinates,
and there are excited states along the space-like directions. As
for the time-like (time-separation between the quarks),
there are no excitations, but there still exist a time-energy uncertainty
without excitation. According to Dirac, it is a c-number time-energy
uncertainty relation.
Can you boost a quark-model wave function to get a parton distribution?
- As the hadron moves fast, the quark distribution becomes
concentrated along one of the light-cone axes. The amplitude of
the oscillation becomes larger, indicating that the spring constant
appears to become weaker. The particles become free!
- The momentum distribution becomes also widespread. This is what
we see in the world through Feynman's parton model.
- The number of partons is infinite because free particles have
continuous momentum distribution as in the case of black-body radiation.
- The major axis of the ellipse measures the period of oscillation. As Feynman observed, the interaction time between the quarks is dilated.

|
| Y. S. Kim, Phys. Rev. Lett. 63 , 348 (1989). |

|
| P. Hussar, Phys. Rev. 23, 2781 (1981). |
We are of course interested to know whether the parton distribution calculated from the covariant oscillator formalism is in agreement with the distribution observed in the real world. This graph will indicate that the answer is YES.
Feynman's Decoherence
- Let us combine all these figures:
Of course these can be explained in terms of mathematical formulas, and they are given in many published papers. The following two review papers may be helpful.
-
Feynman's Decoherence.
Does the Lorentz boost destroy coherence?
- Covariant Oscillators. See Section on Feynman's decoherence in this paper.
-
Feynman's Decoherence.
Does the Lorentz boost destroy coherence?

|
In this picture of the Lorentz-squeezed hadron, the major axis corresponds to the period of oscillation. It tells how often the quarks inside the hadron meet. The minor axis tells how long it takes the external signal to interact with the single quark. If the total energy of the hadron is 1,000 times the mass, the ratio of the major axis to minor axis is 1,000,000. Thus, other quarks in the same hadron do not have a chance to interfere with the quark interacting with the external signal.
Let us look at this figure. If you are not
familiar with this figure,
Click here for explanation.
As the hadron is boosted, both the space-time and momentum-energy wave
functions exhibit the Lorentz-squeeze. As a consequence, quarks
become like massless particles moving with the speed of light.
Because of the wide-spread longitudinal distribution, the spring
constant appears like very weak, and quarks appear like free particles.
At the same time, the momentum distribution becomes wide-spread. If
free massless particles have a wide-spread momentum distribution, it
is like the black-body radiation: infinite number of massless particles.
Infinite Number of Partons
If the partons
and the quarks are the same particles viewed from different from
different Lorentz frames, why is the number of partons infinite while
the number of quarks is two or three.
If the partons and the quarks are the same particles viewed from
different from different Lorentz frames, why is the number of partons
infinite while the number of quarks is two or three.
Boiling Quarks
In his 1972 book on statistical mechanics,
said
-
When we solve a quantum-mechanical problem, what we really do
is divide the universe into two parts - the system in which we are
interested and the rest of the universe. We then usually act as if
the system in which we are interested comprised the entire universe.
To motivate the use of density matrices, let us see what happens
when we include the part of the universe outside the system.
The Bohr radius is an important quantity in quantum mechanics. It is a space-like separation between two particles. However, if the system is boosted, the time-like separation becomes prominent. This problem goes back to Bohr and Einstein. They met often, but they never discussed this issue. Click here for a story.
Since there are no theoretical tools to deal with this problem, this variable is in the Feynman's rest of the universe.
On the other hand, von Neumann's approach to entropy tells us how to deal with the variable we do not measure. If they are not measured, they appear as an entropy increase. Let us look at this figure.
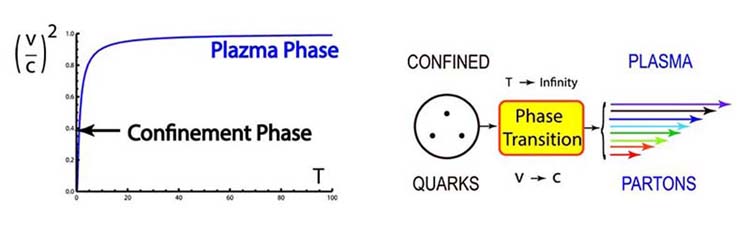
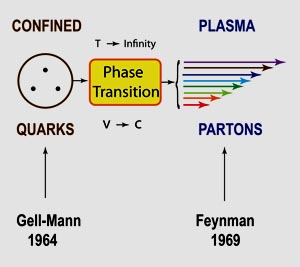
Click here for detailed
calculations. The entropy increase means an increase in temperature.
This thus leads to the following figure the phase transition from
the confined state to a plasma state.

My high-School Background

| |
|