Bose and Einstein

He was also interested in Einstein's research line in statistical physics. Einstein was very strong there also. In 1906, he derived the specific heat of solid using equal-spaced discrete energy spectra. This equal spacing later became oscillator energy levels in quantum mechanics.

Inspired by the photon picture of light waves, Bose was interested deriving Planck's radiation formula, which Planck obtained largely by guessing. Using the particle picture of Einstein, Bose was able to derive the radiation formula by systematically developing a statistics of massless particles without the constraint of particle number conservation. He was quite successful, but was not able to publish his work, because no journals in Europe would accept his paper.

In 1924, Bose wrote to Einstein (in Germany) explaining his work and enclosed his manuscript written in English. Einstein was so happy with Bose's work that he translated the manuscript into German and arranged its publication in Zeitschrift f. Physik (the most prestigious physics journal at that time). Furthermore, in 1926, Einstein completed the Bose-Einstein statistics by extending Bose's work to the case of massive particles with particle-number conservation.

The Bose-Einstein statistics was not completely without troubles, because not all the particles obey this statistics. It was Paul A. M. Dirac who found out that the Bose-Einstein system particles are totally symmetric under permutation of particles. This observation of course led to the Fermi-Dirac statistics.

It is interesting to note how intensely Dirac was interested in permutations from his book entitled "Principles of Quantum Mechanics." Pleas click here for an interesting story about Dirac's permutations.

Let us go back to the photon statistics formula derived by Bose. There is a factor "2" sitting on the numerator of this formula. The usual explanation is that it is because photons are massless particles. Then why not 1 or 3 ? Bose argued that the photon can have two degenerate states. This eventually led to the concept of photon spin parallel or anti-parallel to the momentum.

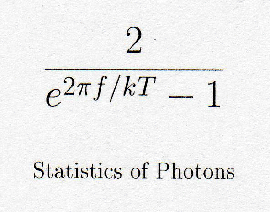
The question of why the photon spin should be only along the direction of momentum has a stormy history. Eugene Wigner (1939) showed that the internal space-time symmetry of massless particles is isomorphic to the symmetry of two-dimensional Euclidean space consisting of one rotation and two translational degrees of freedom. It is not difficult to associate the rotational degree with the photon spin either parallel or anti-parallel to the momentum, but what physics is associated with the translational degrees of freedom.

These translational degrees were later identified as gauge transformations. This does not solve the whole problem because there is one gauge degree of freedom while there are two translational degrees of freedom. How do they collapse into the one gauge degree of freedom? This problem was not completely solved until 1990. Click here for the paper containing the answer to this question.

I would like to thank Satindar Bhagat and Jogesh Pati for telling me about Satyendranath Bose. I am particularly grateful to Jogesh for emphasizing the importance of the factor 2 in Bose's formula.

Y. S. Kim (2005.2.12)